Semantic DB
The SDB is a long running project that started with a simple premise. Can we build a programming language where everything is either a node or a link between nodes? In other words, we are trying to design a graph database language, but hopefully with a unique and useful approach. The big motivation is the human brain, the grandaddy of all graph networks. There is vastly more going on in brains than just nodes and links between nodes, but we still feel our language is a step in the direction of describing brain like systems. Our language is particularly good at sparse representations, and symbolic representations of knowledge. Though there tends to be too much processing overhead for fast manipulation of dense representations, but that domain is already well represented by other approaches.
So, what exactly is a node? Well, a node needs two things really, a label, and an activation level. A label so we know which node we are talking about, and a float to represent how active that node is at a given time. Which to us sounds an awful lot like a synapse in a brain, or at least, a simplified representation of a synapse. Brains and synapses are messy, so we simplified them a bit for this work. Then we can associate a given label with a given synapse, and the float activation level with the firing rate of that synapse over some small time window. If the synapse is not active at that time, the activation level is 0, and if the synapse is acting as an inhibition, then the activation level will be negative.
OK, but how do you represent nodes in your language? Well, we borrow an idea from the famous physicist Paul Dirac, the so called bra-ket notation, used to describe the mathematics of quantum states. In his scheme kets (and bra's) represent quantum states, and the corresponding "activation levels" are complex numbers. For technical reasons we don't need bra's in this work, and we can restrict ourselves to real numbers (floats). The mathematics of space-time might need complex numbers, but we don't. It is often useful to have node labels that correspond to concepts. Like the colour red, the fruit apple, the person Fred Smith, the number 37, the state of hungry, tired, or sad, and so on. Simply enough, we represent them as:
|colour: red>
|fruit: apple>
|person: Fred Smith>
|number: 37>
|hungry>
|tired>
|sad>
OK. Simple enough. But where are the activation levels? Well, in these examples, they are implicit. If an activation level is not given then it is assumed to have value of 1 (ie, an activation level of 100%). If instead we want to represent "a little hungry" or "very tired" or "somewhat sad" then we could write:
0.3|hungry>
0.95|tired>
0.5|sad>
Corresponding to activation levels of 30%, 95% and 50% respectively. An aside on node label conventions. It is sometimes useful to include a category for an object represented by a ket. In the above examples, those categories are "colour", "fruit", "person" and "number". But it is more often useful to leave out the category prefix, and leave it as implicit. Usually it is simple enough to write an operator that maps back and forth between the two conventions. Not that we have defined operators yet.
Now, a system with a single node is not all that useful. So how do we represent a state with multiple simultaneously active nodes? It turns out that kets have a natural addition operator. If you have two apples and you "add" three apples, you have five apples. If you have a system with 2 apples combined with a system of 5 oranges and 7 bananas then you have:
2|apple> + 5|orange> +
7|banana>
Again, going back to quantum mechanics, we call this object a superposition. The motivation for calling it a superposition is say the "Schroedinger cat" superposition. Ie, is the cat alive or dead before we open the box?
0.5|yes> + 0.5|no>
And just like addition has the "identity element" 0, we also need an identity element for ket addition. We call it the empty ket:
|>
The empty ket has the property that you can add it to any superposition and it will not change that superposition, and corresponds to a system with no nodes active. At first glance you might think why do we need this thing? But it turns out to be useful all over the place. For example, when an operator is applied to a system and it disactivates a node.
In the early versions of this project, that was all we used to represent states. But we can add significantly more power to our notation if we introduce another component: sequences. A sequence in our notation is a time ordered list of kets or superpositions, represented using the "." as an infix operator. So a simple example is the spelling of "Smith", represented as:
|S> . |m> . |i> . |t> .
|h>
Noting that sequences are "time ordered", but the exact time step between each ket/superposition is implicit. At this point we feel there is no need for explicit time steps, and if there were the simplest approach would be implementing an operator that zips together two sequences, one with the ket/superpositions, and the other with the corresponding time step.
That is it! That is all we need to represent the state of a system of nodes, with corresponding activation levels. But we promised links between nodes too. Hence we introduce operators, or at least, the simplest examples of operators. An operator in our notation is an object that takes one system described by kets, and maps it to another state described by kets. The power of this idea is that because everything is a ket, this operator mapping can be chained. So if we have an operator that changes the system from state A to state B, and an operator that changes the state from B to C, and finally one from C to D, we can trivially chain them to form an operator that maps the system from state A to state D.
But let us step back a bit, and introduce the learn rule. A learn rule is a type of associative memory (with some similarity to triple stores, or RDF), and is a central component of the SDB language. It allows us to associate a ket, superposition or sequence with respect to a given ket. Indeed, combined with other language features, we can do much more besides! We label this association with a text string. And this string becomes an operator that maps the given ket to the object on the right hand side of the learn rule. For example, we can have operators that map a person from them to their age, to their list of friends, or to the spelling of their name:
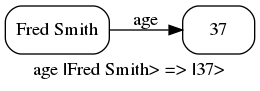
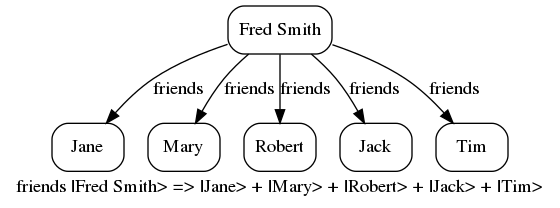

Here we have given both the visual representation and the text representation of some sample learn rules (where we used graphviz and the dot language to create our visualizations). To actually do anything with learn rules, we need to introduce the SDB shell. The open source code for this is available at github. Once installed, we invoke the shell from the command line (we use WSL (Windows Subsystem for Linux)):
$ ./SDB3_1 --interactive
Welcome to the Semantic DB version 3.1.1 shell.
Last updated 18th June 2021.
Type h for help.
Online info for the SDB language at
http://semantic-db.org/docs/usage3/
sa:
Let's enter in the above sample learn rules:
sa: age |Fred Smith> =>
|37>
sa: friends |Fred Smith> => |Jane> + |Mary> +
|Robert> + |Jack> + |Tim>
sa: spelling |Fred Smith> => |F> . |r> . |e> . |d>
. | > . |S> . |m> . |i> . |t> . |h>
And that is it! We have successfully defined three linear operators that act on the "Fred Smith" ket: "age", "friends" and "spelling". Or in other words, we have added some knowledge to our associative memory system. To query the system, we apply the desired operator to the desired ket. Say we want to know Fred's friends:
sa: friends |Fred Smith> |Jane> + |Mary> + |Robert> + |Jack> + |Tim>
How about we next learn the ages of Fred's friends by using these learn rules:
sa: age |Jane> => |25>
sa: age |Mary> => |26>
sa: age |Robert> => |31>
sa: age |Jack> => |29>
sa: age |Tim> => |37>
Then we can ask the age of someone individually, in this case Robert, or we could use operator chaining, and operator linearity, to see the ages of all of Fred's friends at once. So, let's do that:
sa: age |Robert> |31> sa: age friends |Fred Smith> |25> + |26> + |31> + |29> + |37> Finally, we are starting to see a little of the power of this scheme. It takes a little bit of setup work to define operators, but once we have them they are a powerful means of representing changes in the state of a system. In this case we step from a single active node the "Fred Smith" node, to the collection of nodes that represent Fred's friends, to the collection of nodes that represent their ages. This scheme very easily and compactly describes such systems as mapping words to their plurals and back, or stepping through family trees. For example the query for Sam's mother's father's sister would be:
sa: sister father mother |Sam>
For those a little more math inclined, we can note that applying these linear operators to a system state is in fact sparse matrix multiplication. So the "friends" operator can be interpreted as a transition matrix from people to their vector of friends. And the "age" operator is a transition matrix from people to their ages. The advantage of our scheme is that we don't require a dense representation, since in most cases the data is actually sparse. Say you had the ages of 300 people, with age ranges 1 to 100, a dense representation would require a 300*100 matrix. But almost all values in that matrix would be 0. Another example is the dataset that maps actors to the list of movies they have starred in, and movies to the list of actors in that movie. A naive dense matrix representation would be huge, with the vast majority of the entries 0. In the SDB language we can much more efficiently represent this knowledge. On the other hand, systems like artificial neural nets usually require dense representations, and for that the SDB language is less than ideal.
There is much, much more the SDB language, see the usage docs for terse descriptions of the language features. For example, only the simplest operators are linear, most of them are much more "complicated". But the above serves as an introduction to the founding principles of the SDB language. Don't forget to check the bottom of the usage docs page for example files, and the examples page for explanations of some of the examples.