The Semantic DB Project write up.
Knowledge Representation and a language to reason with that knowledge
AKA
Towards a Semantic Web
Contents:
Let's start with a series of examples of the BKO (bra-ket-op) scheme:
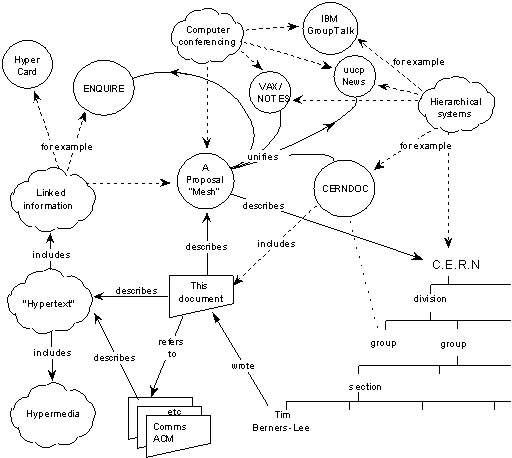
Now in BKO form:
www-proposal.sw
|context> => |context: www proposal>
describes |document: www proposal> => |"Hypertext"> + |A Proposal "Mesh">
refers-to |document: www proposal> => |Comms ACM>
describes |Comms ACM> => |"Hypertext">
includes |"Hypertext"> => |Linked information> + |Hypermedia>
for-example |Linked information> => |Hyper Card> + |ENQUIRE> + |A Proposal "Mesh">
describes |a proposal "mesh"> => |CERN>
unifies |a proposal "mesh"> => |ENQUIRE> + |VAX/NOTES> + |uucp News> + |CERNDOC>
examples |Computer conferencing> => |IBM GroupTalk> + |uucp News> + |VAX/NOTES> + |A Proposal "Mesh">
for-example |Hierarchical systems> => |CERN> + |CERNDOC> + |Vax/Notes> + |uucp News> + |IBM GroupTalk>
includes |CERNDOC> => |document: www proposal>
wrote |person: Tim Berners-Lee> => |document: www proposal>

in BKO form:
methanol.sw
|context> => |context: methanol>
molecular-pieces |molecule: methanol> => |methanol: 1> + |methanol: 2> + |methanol: 3> + |methanol: 4> + |methanol: 5> + |methanol: 6>
atom-type |methanol: 1> => |atom: H>
bonds-to |methanol: 1> => |methanol: 4>
atom-type |methanol: 2> => |atom: H>
bonds-to |methanol: 2> => |methanol: 4>
atom-type |methanol: 3> => |atom: H>
bonds-to |methanol: 3> => |methanol: 4>
atom-type |methanol: 4> => |atom: C>
bonds-to |methanol: 4> => |methanol: 1> + |methanol: 2> + |methanol: 3> + |methanol: 5>
atom-type |methanol: 5> => |atom: O>
bonds-to |methanol: 5> => |methanol: 4> + |methanol: 6>
atom-type |methanol: 6> => |atom: H>
bonds-to |methanol: 6> => |methanol: 5>
-- quick look in the console:
sa: load methanol.sw
sa: atom-type molecular-pieces |molecule: methanol>
4.000|atom: H> + |atom: C> + |atom: O>

in BKO:
simple-network.sw
O |a1> => |a2>
O |a2> => |a3>
O |a3> => |a4>
O |a4> => |a5>
O |a5> => |a6>
O |a6> => |a7>
O |a7> => |a8>
O |a8> => |a9>
O |a9> => |a10>
O |a10> => |a1> + |b1>
O |b1> => |b2>
O |b2> => |b3>
O |b3> => |b4>
O |b4> => |b5>
O |b5> => |b6>
O |b6> => |b7>
O |b7> => |b1>
as a matrix:
sa: matrix[O]
[ a1 ] = [ 0 0 0 0 0 0 0 0 0 1.00 0 0 0 0 0 0 0 ] [ a1 ]
[ a2 ] [ 1.00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] [ a2 ]
[ a3 ] [ 0 1.00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] [ a3 ]
[ a4 ] [ 0 0 1.00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ] [ a4 ]
[ a5 ] [ 0 0 0 1.00 0 0 0 0 0 0 0 0 0 0 0 0 0 ] [ a5 ]
[ a6 ] [ 0 0 0 0 1.00 0 0 0 0 0 0 0 0 0 0 0 0 ] [ a6 ]
[ a7 ] [ 0 0 0 0 0 1.00 0 0 0 0 0 0 0 0 0 0 0 ] [ a7 ]
[ a8 ] [ 0 0 0 0 0 0 1.00 0 0 0 0 0 0 0 0 0 0 ] [ a8 ]
[ a9 ] [ 0 0 0 0 0 0 0 1.00 0 0 0 0 0 0 0 0 0 ] [ a9 ]
[ a10 ] [ 0 0 0 0 0 0 0 0 1.00 0 0 0 0 0 0 0 0 ] [ a10 ]
[ b1 ] [ 0 0 0 0 0 0 0 0 0 1.00 0 0 0 0 0 0 1.00 ] [ b1 ]
[ b2 ] [ 0 0 0 0 0 0 0 0 0 0 1.00 0 0 0 0 0 0 ] [ b2 ]
[ b3 ] [ 0 0 0 0 0 0 0 0 0 0 0 1.00 0 0 0 0 0 ] [ b3 ]
[ b4 ] [ 0 0 0 0 0 0 0 0 0 0 0 0 1.00 0 0 0 0 ] [ b4 ]
[ b5 ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 1.00 0 0 0 ] [ b5 ]
[ b6 ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.00 0 0 ] [ b6 ]
[ b7 ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1.00 0 ] [ b7 ]

in BKO:
binary-tree-with-child.sw
text |x> => |start node>
left |x> => |0>
right |x> => |1>
child |x> => |0> + |1>
text |0> => |first child node>
left |0> => |00>
right |0> => |10>
child |0> => |00> + |10>
text |1> => |second child node>
left |1> => |01>
right |1> => |11>
child |1> => |01> + |11>
text |00> => |third child node>
left |00> => |000>
right |00> => |100>
child |00> => |000> + |100>
text |10> => |fourth child node>
left |10> => |010>
right |10> => |110>
child |10> => |010> + |110>
text |01> => |fifth child node>
left |01> => |001>
right |01> => |101>
child |01> => |001> + |101>
text |11> => |sixth child node>
left |11> => |011>
right |11> => |111>
child |11> => |011> + |111>
as a matrix:
sa: matrix[child]
[ 0 ] = [ 0 0 0 0 0 0 0 1.00 ] [ * ]
[ 00 ] [ 0 1.00 0 0 0 0 0 0 ] [ 0 ]
[ 000 ] [ 0 0 1.00 0 0 0 0 0 ] [ 00 ]
[ 001 ] [ 0 0 0 1.00 0 0 0 0 ] [ 01 ]
[ 01 ] [ 0 0 0 0 1.00 0 0 0 ] [ 1 ]
[ 010 ] [ 0 0 0 0 0 1.00 0 0 ] [ 10 ]
[ 011 ] [ 0 0 0 0 0 0 1.00 0 ] [ 11 ]
[ 1 ] [ 0 0 0 0 0 0 0 1.00 ] [ x ]
[ 10 ] [ 0 1.00 0 0 0 0 0 0 ]
[ 100 ] [ 0 0 1.00 0 0 0 0 0 ]
[ 101 ] [ 0 0 0 1.00 0 0 0 0 ]
[ 11 ] [ 0 0 0 0 1.00 0 0 0 ]
[ 110 ] [ 0 0 0 0 0 1.00 0 0 ]
[ 111 ] [ 0 0 0 0 0 0 1.00 0 ]
c = new_context("grid play")
def ket_elt(j,i):
return ket("grid: " + str(j) + " " + str(i))
# Makes use of the fact that context.learn() ignores rules that are the empty ket |>.
def ket_elt_bd(j,i,I,J):
# finite universe model:
# if i <= 0 or j <= 0 or i > I or j > J:
# return ket("",0)
# torus model:
i = (i - 1)%I + 1
j = (j - 1)%J + 1
return ket("grid: " + str(j) + " " + str(i))
def create_grid(c,I,J):
c.learn("dim-1","grid",str(I))
c.learn("dim-2","grid",str(J))
for j in range(1,J+1):
for i in range(1,I+1):
elt = ket_elt(j,i)
c.add_learn("elements","grid",elt)
c.learn("N",elt,ket_elt_bd(j-1,i,I,J))
c.learn("NE",elt,ket_elt_bd(j-1,i+1,I,J))
c.learn("E",elt,ket_elt_bd(j,i+1,I,J))
c.learn("SE",elt,ket_elt_bd(j+1,i+1,I,J))
c.learn("S",elt,ket_elt_bd(j+1,i,I,J))
c.learn("SW",elt,ket_elt_bd(j+1,i-1,I,J))
c.learn("W",elt,ket_elt_bd(j,i-1,I,J))
c.learn("NW",elt,ket_elt_bd(j-1,i-1,I,J))
a couple of example grid locations:
supported-ops |grid: 4 39> => |op: N> + |op: NE> + |op: E> + |op: SE> + |op: S> + |op: SW> + |op: W> + |op: NW>
N |grid: 4 39> => |grid: 3 39>
NE |grid: 4 39> => |grid: 3 40>
E |grid: 4 39> => |grid: 4 40>
SE |grid: 4 39> => |grid: 5 40>
S |grid: 4 39> => |grid: 5 39>
SW |grid: 4 39> => |grid: 5 38>
W |grid: 4 39> => |grid: 4 38>
NW |grid: 4 39> => |grid: 3 38>
supported-ops |grid: 4 40> => |op: N> + |op: NE> + |op: E> + |op: SE> + |op: S> + |op: SW> + |op: W> + |op: NW>
N |grid: 4 40> => |grid: 3 40>
NE |grid: 4 40> => |grid: 3 41>
E |grid: 4 40> => |grid: 4 41>
SE |grid: 4 40> => |grid: 5 41>
S |grid: 4 40> => |grid: 5 40>
SW |grid: 4 40> => |grid: 5 39>
W |grid: 4 40> => |grid: 4 39>
NW |grid: 4 40> => |grid: 3 39>
factorial.sw
|context> => |context: factorial>
fact |0> => |1>
n-1 |*> #=> arithmetic(|_self>,|->,|1>)
fact |*> #=> arithmetic( |_self>, |*>, fact n-1 |_self>)
fibonacci.sw
|context> => |context: Fibonacci>
fib |0> => |0>
fib |1> => |1>
n-1 |*> #=> arithmetic(|_self>,|->,|1>)
n-2 |*> #=> arithmetic(|_self>,|->,|2>)
fib |*> #=> arithmetic( fib n-1 |_self>, |+>, fib n-2 |_self>)
fib-ratio |*> #=> arithmetic( fib |_self> , |/>, fib n-1 |_self> )
The task:
For numbers 1 through 100,
- if the number is divisible by 3 print Fizz;
- if the number is divisible by 5 print Buzz;
- if the number is divisible by 3 and 5 (15) print FizzBuzz;
- else, print the number.
in BKO:
fizz-buzz.sw
|context> => |context: Fizz-Buzz v1>
|list> => range(|1>,|100>)
fizz-buzz-0 |*> #=> |_self>
fizz-buzz-1 |*> #=> if(arithmetic(|_self>,|%>,|3>) == |0>,|Fizz>,|>)
fizz-buzz-2 |*> #=> if(arithmetic(|_self>,|%>,|5>) == |0>,|Buzz>,|>)
fizz-buzz-3 |*> #=> if(arithmetic(|_self>,|%>,|15>) == |0>,|FizzBuzz>,|>)
map[fizz-buzz-0,fizz-buzz] "" |list>
map[fizz-buzz-1,fizz-buzz] "" |list>
map[fizz-buzz-2,fizz-buzz] "" |list>
map[fizz-buzz-3,fizz-buzz] "" |list>
george.sw
|context> => |context: George>
source |context: George> => |sw-url: http://semantic-db.org/sw-examples/new-george.sw>
-- George is just some fictional character
|person: George> => |word: george>
age |person: George> => |age: 29>
dob |person: George> => |date: 1984-05-23>
hair-colour |person: George> => |hair-colour: brown>
eye-colour |person: George> => |eye-colour: blue>
gender |person: George> => |gender: male>
height |person: George> => |height: cm: 176>
wife |person: George> => |person: Beth>
occupation |person: George> => |occupation: car salesman>
friends |person: George> => |person: Fred> + |person: Jane> + |person: Liz> + |person: Andrew>
mother |person: George> => |person: Sarah>
father |person: George> => |person: David>
sisters |person: George> => |person: Emily>
brothers |person: George> => |person: Frank> + |person: Tim> + |person: Sam>
email |person: George> => |email: george.douglas@gmail.com>
education |person: George> => |education: high-school>
-- some general rules that apply to all people:
siblings |person: *> #=> brothers |_self> + sisters |_self>
children |person: *> #=> sons |_self> + daughters |_self>
parents |person: *> #=> mother |_self> + father |_self>
uncles |person: *> #=> brothers parents |_self>
aunts |person: *> #=> sisters parents |_self>
aunts-and-uncles |person: *> #=> siblings parents |_self>
cousins |person: *> #=> children siblings parents |_self>
grand-fathers |person: *> #=> father parents |_self>
grand-mothers |person: *> #=> mother parents |_self>
grand-parents |person: *> #=> parents parents |_self>
grand-children |person: *> #=> children children |_self>
great-grand-parents |person: *> #=> parents parents parents |_self>
great-grand-children |person: *> #=> children children children |_self>
immediate-family |person: *> #=> siblings |_self> + parents |_self> + children |_self>
friends-and-family |person: *> #=> friends |_self> + family |_self>
learning-plurals.sw
-- before we have defined anything:
sa: plural |word: cat>
|>
-- in English |> means "I don't know anything about that".
-- define a general rule:
sa: plural |word: *> #=> merge-labels(|_self> + |s>)
-- test it:
sa: plural |word: cat>
|word: cats>
sa: plural |word: dog>
|word: dogs>
-- ok. But what about the irregular forms?
sa: plural |word: mouse>
|word: mouses>
sa: plural |word: foot>
|word: foots>
-- ok. we have a general rule, now define specific rules:
-- learn mouse specific rule:
sa: plural |word: mouse> => |word: mice>
-- learn foot specific rule:
sa: plural |word: foot> => |word: feet>
-- now, try again:
sa: plural |word: mouse>
|word: mice>
sa: plural |word: foot>
|word: feet>
as a matrix:
sa: matrix[plural]
[ word: *s ] = [ 1.00 0 0 ] [ word: * ]
[ word: feet ] [ 0 1.00 0 ] [ word: foot ]
[ word: mice ] [ 0 0 1.00 ] [ word: mouse ]
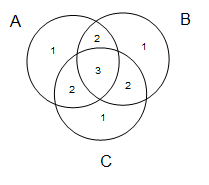
A = {a1,a2,a3,ab,ac,abc}
B = {b1,b2,b3,ab,bc,abc}
C = {c1,c2,c3,ac,bc,abc}
in BKO:
simple-finite-sets.sw
-- NB: coeffs for set elements are almost always in {0,1}
|A> => |a1> + |a2> + |a3> + |ab> + |ac> + |abc>
|B> => |b1> + |b2> + |b3> + |ab> + |bc> + |abc>
|C> => |c1> + |c2> + |c3> + |ac> + |bc> + |abc>
now take a look at set intersection in the console:
sa: intersection(""|A>, ""|B>)
|ab> + |abc>
sa: intersection(""|A>, ""|C>)
|ac> + |abc>
sa: intersection(""|B>, ""|C>)
|bc> + |abc>
sa: intersection(""|A>,""|B>,""|C>)
|abc>
Now observe a correspondence between set intersection and addition of superpositions with coeffs in {0,1}:
-- add our superpositions:
-- NB: the coeffs correspond to the number of sets an element is in, cf. the Venn diagram above.
sa: ""|A> + ""|B> + ""|C>
|a1> + |a2> + |a3> + 2.000|ab> + 2.000|ac> + 3.000|abc> + |b1> + |b2> + |b3> + 2.000|bc> + |c1> + |c2> + |c3>
-- this is the same as union:
sa: clean(""|A> + ""|B> + ""|C>)
|a1> + |a2> + |a3> + |ab> + |ac> + |abc> + |b1> + |b2> + |b3> + |bc> + |c1> + |c2> + |c3>
-- this is the same as intersection:
sa: clean drop-below[3] (""|A> + ""|B> + ""|C>)
|abc>
-- this is a "soft" intersection:
sa: clean drop-below[2] (""|A> + ""|B> + ""|C>)
|ab> + |ac> + |abc> + |bc>
BTW, we also have set-builder (at least in theory, it is not yet implemented).
It looks something like this:
|answer> => yet-another-op another-op |x> in op |object> such that <y|op-sequence|x> >= 0.7
BKO is what I call an "active representation" -- once in this format, a lot of things are relatively easy.
One of the driving forces behind BKO is to collapse all knowledge into one unified representation.
So any machinery we develop for some branch of knowledge often extends easily to other branches.
context.learn(a,b,c)
context.recall(a,b)
eg:
-- learn a rule
sa: a |b> => |c>
-- recall a rule
sa: a |b>
|c>
1) <x||y> == 0 if x != y.
2) <x||y> == 1 if x == y.
3) <!x||y> == 1 if x != y. (NB: the ! acts as a not. cf, the -v switch for grep)
4) <!x||y> == 0 if x == y.
5) <x: *||y: z> == 0 if x != y.
6) <x: *||y: z> == 1 if x == y, for any z.
7) applying bra's is linear. <x|(|a> + |b> + |c>) == <x||a> + <x||b> + <x||c>
8) if a coeff is not given, then it is 1. eg, <x| == <x|1 and 1|x> == |x>
9) bra's and ket's commute with the coefficients. eg, <x|7 == 7 <x| and 13|x> == |x>13
10) in contrast to QM, in BKO operators are right associative only.
<a|(op|b>) is valid and is identical to <a|op|b>
(<a|op)|b> is invalid, and undefined.
11) again, in contrast to QM, <a|op|b> != <b|op|a>^* (a consequence of (10) really)
12) applying projections is linear. |x><x|(|a> + |b> + |c>) == |x><x||a> + |x><x||b> + |x><x||c>
13) kets in superpositions commute. |a> + |b> == |b> + |a>
14) kets in sequences do not commute. |a> . |b> != |b> . |a>
Though maybe in the sequence version of simm, this would be useful:
|a> . |b> = c |b> . c |a>, where usually c is < 1. (yeah, it "bugs out" if you swap it back again, but in practice should be fine)
another example:
|c> . |a> . |b> = c |a> . c |c> . |b>
= c |a> . c |b> . c^2 |c>
15) operators (in general) do not commute. <b|op2 op1|a> != <b|op1 op2|a>
16) if a coeff in a superposition is zero, we can drop it from the superposition without changing the meaning of that superposition.
17) we can arbitrarily add kets to a superposition if they have coeff zero without changing the meaning of that superposition.
18) |> is the identity element for superpositions. sp + |> == |> + sp == sp.
19) the + sign in superpositions is literal. ie, kets add.
|a> + |a> + |a> = 3|a>
|a> + |b> + |c> + 6|b> = |a> + 7|b> + |c>
20) <x|op-sequence|y> is always a scalar/float
21) |x><x|op-sequence|y> is always a ket or a superposition
What are sigmoids? They are a collection of functions that only change the coeffs in superpositions.
Here are a couple of examples:
|f> => absolute-noise[3] 0 range(|x: 0>,|x: 255>)

binary-filter "" |f>
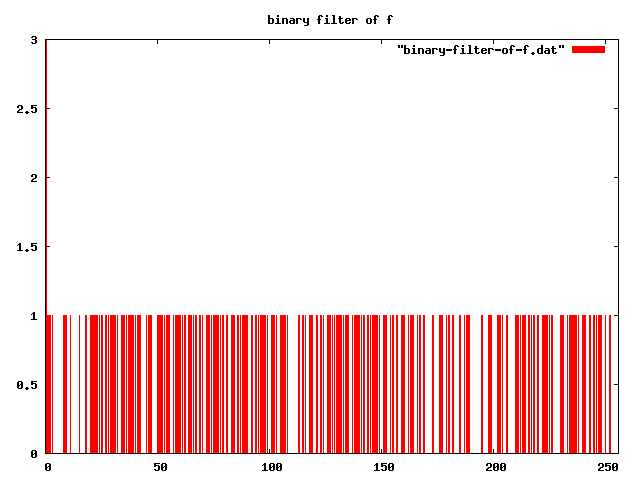
threshold-filter[1] "" |f>
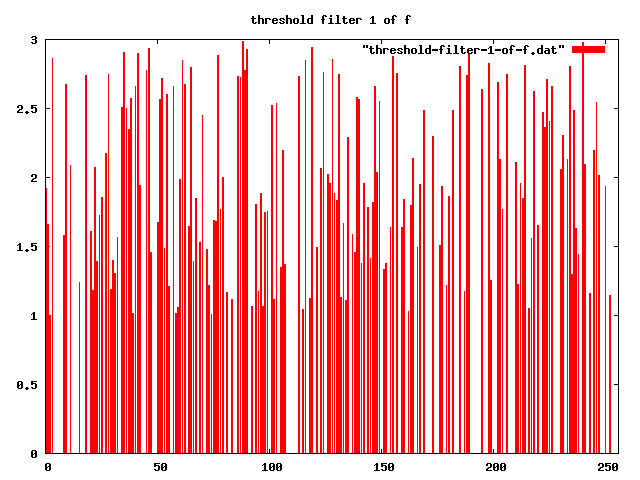
threshold-filter[2] "" |f>
threshold-filter[2.5] "" |f>

-- first, set the context:
sa: context fred friends
-- let's enter in some data:
sa: friends |Fred> => |Sam> + |Harry> + |Liz> + |Rob> + |Emma> + |Mazza>
sa: friends |Sam> => |Eric> + |Smithie> + |Patrick> + |Tom>
sa: friends |Harry> => |Jane> + |Sarah> + |Jean> + |Alicia>
-- let's have a quick play with this data:
-- who are Fred's friends?
sa: friends |Fred>
|Sam> + |Harry> + |Liz> + |Rob> + |Emma> + |Mazza>
-- how many friends does Fred have?
sa: count friends |Fred>
|number: 6>
-- who are Fred's friends of friends?
sa: friends friends |Fred>
|Eric> + |Smithie> + |Patrick> + |Tom> + |Jane> + |Sarah> + |Jean> + |Alicia>
-- how many are there:
sa: count friends^2 |Fred>
|number: 8>
-- six degrees of separation looks like this (if we had the data):
friends^6 |Fred>
-- or, alternatively, one of these:
sa: exp[friends,6] |Fred>
sa: exp-max[friends] |Fred>
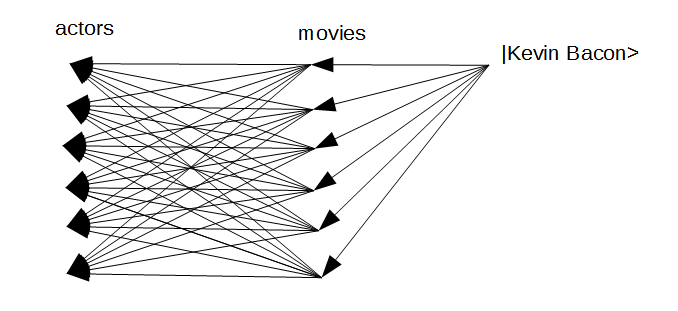
Is as simple as this, assuming a sufficiently powerful computer (here is the result):
kevin-bacon-0 |result> => |actor: Kevin (I) Bacon>
kevin-bacon-1 |result> => actors movies |actor: Kevin (I) Bacon>
kevin-bacon-2 |result> => actors movies actors movies |actor: Kevin (I) Bacon>
The general case is:
kevin-bacon-k |result> => [actors movies]^k |actor: Kevin (I) Bacon>
abc.net.au:



adelaidenow.com.au:



slashdot.org:



smh.com.au:



youtube.com:



These were created by fragmenting html documents at the < and > characters, taking the hash of each fragment, keeping only the last 4 chars of that hash, say, then add up the kets. The advantage of this is that any localized changes in the document do not affect fragments elsewhere in the document. And for the given websites they have largely the same structure from day to day, as we can see by the plots.
sa: load fragment-webpages-64k.sw
sa: |list> => |abc-1-64k> + |abc-2-64k> + |abc-3-64k> + |adelaidenow-1-64k> + |adelaidenow-2-64k> + |adelaidenow-3-64k> + |slashdot-1-64k> + |slashdot-2-64k> + |slashdot-3-64k> + |smh-1-64k> + |smh-2-64k> + |smh-3-64k> + |youtube-1-64k> + |youtube-2-64k> + |youtube-3-64k>
sa: simm-0 |*> #=> 100 (|_self> + similar[hash-64k] |_self>)
sa: map[simm-0,similarity-0] "" |list>
sa: matrix[similarity-0]
[ abc-1-64k ] = [ 100.00 91.52 91.13 29.84 30.17 29.96 27.64 27.57 27.48 38.36 38.93 38.67 21.00 21.04 20.98 ] [ abc-1-64k ]
[ abc-2-64k ] [ 91.52 100.00 91.90 29.83 30.19 29.97 27.62 27.66 27.63 38.43 39.01 38.75 21.11 21.17 21.07 ] [ abc-2-64k ]
[ abc-3-64k ] [ 91.13 91.90 100.00 30.05 30.38 30.19 27.74 27.77 27.63 38.41 39.05 38.77 21.12 21.18 21.12 ] [ abc-3-64k ]
[ adelaidenow-1-64k ] [ 29.84 29.83 30.05 100.00 78.88 78.11 27.26 27.00 27.16 30.55 30.31 30.36 26.91 26.96 27.06 ] [ adelaidenow-1-64k ]
[ adelaidenow-2-64k ] [ 30.17 30.19 30.38 78.88 100.00 83.22 27.37 27.28 27.34 30.46 30.31 30.36 26.97 26.97 27.00 ] [ adelaidenow-2-64k ]
[ adelaidenow-3-64k ] [ 29.96 29.97 30.19 78.11 83.22 100.00 27.17 27.05 27.11 30.28 30.16 30.16 26.96 26.84 26.98 ] [ adelaidenow-3-64k ]
[ slashdot-1-64k ] [ 27.64 27.62 27.74 27.26 27.37 27.17 100.00 77.37 77.25 29.76 29.67 29.75 22.16 22.14 22.17 ] [ slashdot-1-64k ]
[ slashdot-2-64k ] [ 27.57 27.66 27.77 27.00 27.28 27.05 77.37 100.00 78.52 29.55 29.53 29.60 21.71 21.64 21.73 ] [ slashdot-2-64k ]
[ slashdot-3-64k ] [ 27.48 27.63 27.63 27.16 27.34 27.11 77.25 78.52 100.00 29.82 29.70 29.87 21.98 21.99 22.00 ] [ slashdot-3-64k ]
[ smh-1-64k ] [ 38.36 38.43 38.41 30.55 30.46 30.28 29.76 29.55 29.82 100.00 84.04 85.28 22.45 22.47 22.58 ] [ smh-1-64k ]
[ smh-2-64k ] [ 38.93 39.01 39.05 30.31 30.31 30.16 29.67 29.53 29.70 84.04 100.00 85.80 22.18 22.17 22.23 ] [ smh-2-64k ]
[ smh-3-64k ] [ 38.67 38.75 38.77 30.36 30.36 30.16 29.75 29.60 29.87 85.28 85.80 100.00 22.22 22.27 22.24 ] [ smh-3-64k ]
[ youtube-1-64k ] [ 21.00 21.11 21.12 26.91 26.97 26.96 22.16 21.71 21.98 22.45 22.18 22.22 100.00 90.16 90.12 ] [ youtube-1-64k ]
[ youtube-2-64k ] [ 21.04 21.17 21.18 26.96 26.97 26.84 22.14 21.64 21.99 22.47 22.17 22.27 90.16 100.00 90.67 ] [ youtube-2-64k ]
[ youtube-3-64k ] [ 20.98 21.07 21.12 27.06 27.00 26.98 22.17 21.73 22.00 22.58 22.23 22.24 90.12 90.67 100.00 ] [ youtube-3-64k ]
we can make a lot of progress in pattern recognition if we can find mappings from objects to well-behaved, deterministic, distinctive superpositions.
where:
well-behaved means similar objects return similar superpositions
deterministic means if you feed in the same object, you get essentially the same superposition. (There is some lee-way in that it doesn't have to be 100% identical on each run, but close.)
distinctive means different object types have easily distinguishable superpositions
(which are all satisfied by the web-page example)
Let's define them:
First, we say x is near y if metric[x,y] <= t for a metric of your choice, and some threshold t.
Then a linear bridging set is a set {x0,x1,x2,x3,...,xn} such that:
1) x_k is near x_k+1, for all k in {0,1,...,n}
2) x_0 is not near x_n
A general bridging set is a set {x0,x1,x2,x3,...,xn} such that:
1) for every j in {0,1,...,n}, x_j is near an x_k for some k != j in {0,1,...,n}. -- ie, every element in the set is near some other element in the set
2) there may exist j,k pairs such that x_j is not near x_k

where A is a linear bridging set, and B and C are general bridging sets.
OK. So what is the point of mentioning brdiging sets? Well, it motivates the categorize code.
Categorize maps a set of elements into disjoint bridging sets.
Here is the result for webpage fragments:
sa: load fragment-webpages-64k.sw
sa: categorize[hash-64k,0.7,result]
sa: dump |result>
category-0 |result> => |youtube-3-64k> + |youtube-2-64k> + |youtube-1-64k>
category-1 |result> => |smh-3-64k> + |smh-2-64k> + |smh-1-64k>
category-2 |result> => |abc-1-64k> + |abc-2-64k> + |abc-3-64k>
category-3 |result> => |slashdot-3-64k> + |slashdot-1-64k> + |slashdot-2-64k>
category-4 |result> => |adelaidenow-3-64k> + |adelaidenow-2-64k> + |adelaidenow-1-64k>
find-topic looks up frequency lists, and finds the best match.
sa: load names.sw
sa: find-topic[names] |fred>
63.294|male name> + 28.418|last name> + 8.288|female name>
sa: find-topic[names] |emma>
90.323|female name> + 9.677|last name>
sa: find-topic[names] |george>
45.902|male name> + 40.073|last name> + 14.026|female name>
sa: find-topic[names] |simon>
63.871|last name> + 36.129|male name>
sa: find-topic[names] |thompson>
100.000|last name>
-- now apply this to a handful of wikipedia pages we have converted to word frequency lists:
-- (if we had the computational power it would be nice to try this on all of the English wikipedia)
sa: load WP-word-frequencies.sw
sa: find-topic[words] |wikipedia>
18.539|WP: US presidents> + 18.539|WP: particle physics> + 16.479|WP: rivers> + 16.479|WP: physics> + 16.479|WP: country list> + 13.483|WP: Australia>
sa: find-topic[words] |adelaide>
74.576|WP: Adelaide> + 25.424|WP: Australia>
sa: find-topic[words] |sydney>
60.241|WP: Australia> + 39.759|WP: Adelaide>
sa: find-topic[words] |canberra>
100.000|WP: Australia>
sa: find-topic[words-3] |university of adelaide>
76.923|WP: Adelaide> + 23.077|WP: Australia>
sa: find-topic[words-2] |river nile>
100.000|WP: rivers>
sa: find-topic[words] |physics>
54.237|WP: physics> + 45.763|WP: particle physics>
sa: find-topic[words-2] |particle physics>
60.000|WP: particle physics> + 40.000|WP: physics>
sa: find-topic[words] |electron>
62.791|WP: particle physics> + 37.209|WP: physics>
sa: find-topic[words-2] |quantum mechanics>
62.500|WP: physics> + 37.500|WP: particle physics>
sa: find-topic[words-2] |bill clinton>
100.000|WP: US presidents>
sa: find-topic[words-2] |george bush> -- no match on the exact phrase.
|> -- probably because of the need to disambiguate between father and son.
sa: find-topic[words] (|george> + |bush>)
67.705|WP: US presidents> + 22.363|WP: Australia> + 9.932|WP: Adelaide>
sa: find-topic[words-2] |richard nixon>
100.000|WP: US presidents>
sa: find-topic[words-2] |thomas jefferson>
100.000|WP: US presidents>
sa: find-topic[words] |reagan>
100.000|WP: US presidents>
So, what is an active buffer?
It contains a buffer of the latest input, then tries to find matching patterns with known objects.
-- load some data:
sa: load internet-acronyms.sw
-- read a short sentence:
sa: read |text: fwiw I think it is all fud imho, lol. thx.>
|word: fwiw> + |word: i> + |word: think> + |word: it> + |word: is> + |word: all> + |word: fud> + |word: imho> + |word: lol> + |word: thx>
-- apply active buffer to this:
sa: active-buffer[7,0] read |text: fwiw I think it is all fud imho, lol. thx.>
2.593|phrase: For What It's Worth> + 6.038|phrase: Fear, Uncertainty, Doubt> + 5.279|phrase: In My Humble Opinion> + 4.186|phrase: Laughing Out Loud> + 2.593|phrase: Thanks>
Breakfast menu example (an sw form of this xml version):
sa: load some data:
sa: load next-breakfast-menu.sw
sa: description |food: Homestyle Breakfast>
|text: "Two eggs, bacon or sausage, toast, and our ever-popular hash browns">
-- read the description for Homestyle Breakfast
sa: read description |food: Homestyle Breakfast>
|word: two> + |word: eggs> + |word: bacon> + |word: or> + |word: sausage> + |word: toast> + |word: and> + |word: our> + |word: ever-popular> + |word: hash> + |word: browns>
-- apply active-buffer to this:
sa: active-buffer[7,1] read description |food: Homestyle Breakfast>
|number: 2> + |food: eggs> + |food: bacon> + |food: sausage> + |food: toast> + |food: hash browns>
Fred/Mary/pregnancy example:
-- first load up some knowledge:
sa: |person: Fred Smith> => |word: fred> + |word: freddie> + |word: simth> + |word: smithie> -- various names and nick-names
sa: |person: Mary> => |word: mazza> -- just a nick-name
sa: |greeting: Hey!> => |word: hey>
sa: |question: what is> => |word: what's>
sa: |direction: up> => |word: up>
sa: |phrase: having a baby> => read |text: having a baby>
sa: |phrase: in the family way> => read |text: in the family way>
sa: |phrase: up the duff> => read |text: up the duff>
sa: |phrase: with child> => read |text: with child>
sa: |concept: pregnancy> => |phrase: having a baby> + |phrase: in the family way> + |phrase: up the duff> + |phrase: with child>
-- now start playing with it:
sa: active-buffer[7,0] read |text: Hey Freddie what's up?>
2.083|greeting: Hey!> + 1.500|person: Fred Smith> + 2.917|question: what is> + 2.083|direction: up> + 1.250|phrase: up the duff>
-- up the duff is in there because of the word "up"
-- now test phrase matching a concept, in this case phrases that mean pregnant.
sa: active-buffer[7,0] read |text: Hey Mazza, you with child, up the duff, in the family way, having a baby?>
2.593|greeting: Hey!> + 4.186|person: Mary> + 11.586|phrase: with child> + 6.857|direction: up> + 23.414|phrase: up the duff> + 25.000|phrase: in the family way> + 9.224|phrase: having a baby>
-- one more layer of active-buffer:
sa: active-buffer[7,0] active-buffer[7,0] read |text: Hey Mazza, you with child, up the duff, in the family way, having a baby?>
11.069|concept: pregnancy>
Recognize a face, even if you only see part of it:
-- define the features of a face:
sa: |body part: face> => 2|eyes> + |nose> + 2|ears> + 2|lips> + |hair>
-- even if we only have a couple of pieces of the face, we can still recognize it as a face
sa: active-buffer[7,0] (2|eyes> + |nose>)
0.750|body part: face>
-- again, hair, nose and lips is enough to say we have a face:
sa: active-buffer[7,0] (|hair> + |nose> + |lips>)
1.625|body part: face>
-- this time we see all parts of the face:
sa: active-buffer[7,0] (2|eyes> + |nose> + 2|ears> + 2|lips> + |hair>)
7.125|body part: face>
- map each neuron to a ket
- map firing frequency to the coeff of that ket
- measure neuron firing value using bras
- synapses + neurotransmitters roughly map to sigmoids
Perhaps something like this:

where big circles are neurons, little circles are synapses, and lines are axons and dendrites.
- complete, efficient, open source implementation of the BKO scheme
- a swc (semantic web code) language for when BKO is not quite enough
- an internet scale semantic web
- some scheme to allow others to write and share semantic-db functions
sa: h
q, quit, exit quit the agent.
h, help print this message
context print list of context's
context string set current context to string
reset reset back to completely empty console
Warning! you will lose all unsaved work!
dump print current context
dump exact print current context in exact mode
dump multi print context list
dump self print what we know about the default ket/sp
dump ket/sp print what we know about the given ket/sp
display (relatively) readable display of current context
display ket/sp (relatively) readable display about what we know for the ket/sp
freq convert current context to frequency list
mfreq convert context list to frequency list
load file.sw load file.sw
save file.sw save current context to file.sw
save multi file.sw save context list to file.sw
files show the available .sw files
cd change and create if necessary the .sw directory
ls, dir, dirs show the available directories
create inverse create inverse for current context
create multi inverse create inverse for all context in context list
x = foo: bah set x (the default ket) to |foo: bah>
id display the default ket/superposition
s, store set x to the result of the last computation
. repeat last computation
i interactive history
history show last 30 commands
history n show last n commands
save history save console history to file
-- comment ignore, this is just a comment line.
if none of the above process_input_line(C,line,x)
created: 1/11/2014
updated: 23/11/2014
by Garry Morrison
email: garry -at- semantic-db.org



























